平均方法、すなわち「重量平均法による最確値の計算」を行う必要がある。 ※ 重量(ちょうりょう又はじゅうりょう)(「重み」とも呼ぶ)測定値の信用度。重量は測量の場合、観測方法や路 線長等により決定される。 定义 来自维基百科 指数移动平均(exponential moving average,EMA或EWMA)是以指数式递减加权的移动平均。 各数值的加权影响力随时间而指数式递减,越近期的数据加权影响力越重,但较旧的数据也给予一定的加权值 设时刻 t {t} t的实际数值为 θ t \theta_{t} θt , 时刻 t 調和平均はそのうちの1つです。 と 30 30 の「普通の平均」は \dfrac {30} {2}=25 2 30

算術平均 相加平均 と加重平均の違いは 重み ってナニ データ分析の解説 Haku1569 Excel でらくらく データ分析
平均の公式
平均の公式-TVアニメ「私、能力は平均値でって言ったよね! 」公式サイト 「私、能力は平均値でって言ったよね! 公式ガイドブック」3月16日発売! 「私、能力は平均値でって言ったよね! 」Bluray 第3集ジャケット&特典詳細公開! 「私、能力 平均发展水平(Average level of development)平均发展水平又称"序时平均数"、"动态平均数",是时间序列中各项发展水平的平均数,反映现象在一段时期中发展的一般水平。序时平均数作为一种平均数,与静态平均数有相同点,即它们都抽象了现象的个别差异,以反映现象总体的一般水平。
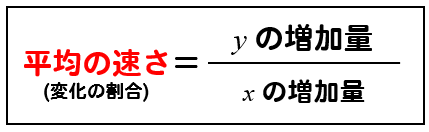



中3 数学 平均の速さの求め方を解説 数スタ
步骤 1:计算加权平均值 结果的加权平均值是通过将样本大小与肯定回答比率作为因素考虑计算得出的。这有助于在两个测试结果之间创建更均衡的比较。用于计算加权平均值的一般公式如下所示:SUM (Weight * Value) / SUM (Weight)最大値、平均値、実効値の関係は、よく理解しておきましょう。 おまけ こんな語句も試験には出てきますので頭の片隅にでも入れておいてください。 、 正弦波交流電流の最大値を Im 、実効値を Ie 、平均値を Ia とすると、波形率は約111になる。第2版 02, 11/6 第3版 04, 9/14 第4版 08, 5/1 情報処理技術社試験の中で良く出て来る「待ち行列」理論を,直感的に覚えやすく解説してみました. 何度もトライしたけど待ち行列が理解できない人向けです. 正確な定義や論理展開は重視せず,いかに効率
日経平均公式ガイドブック 世界中の投資家から注目されてきた「日経平均」も10年で満60歳。 何をどう平均したものなのか、実体経済とどう結びついてきたか、投資にどう役立てればいいのか─―意外と知らない「使い方」をやさしく解説します。 株がわかる! 日経平均公式ガイドブック 書籍, マネー・投資 日本経済新聞社インデックス事業室 編 11 相加平均と相乗平均の大小関係(公式) 2つの実数 \( a,b \) \((a≧0,b≧0)\)について、 \( \displaystyle \frac{ab}{2} \) を 相加平均 といいます。 一方、\( \sqrt{ab} \) を 相乗平均 といいます。 このとき、相加平均と相乗平均には、以下の関係が成り立ちます。公式:加权平均数=(x1f1 x2f2 xkfk)/n,其中f1 f2 fk=n,f1,f2,,fk叫做权,通过数和权的乘积来计算。
次に、この仮平均との差についての平均を求めます。 $$差の平均=()\div4=24\div 4=6$$ これは何を表しているかというと 実際の平均は、あなたの決めた仮平均から+6差がありますよ! ってことを示しています。 だから、求めたかった平均は $$平均=1306=136㎝$$2乗の平均を求めます。 \(\displaystyle \frac{40^{2}50^{2}60^{2}60^{2}90^{2}}{5}\) \(=\displaystyle \frac{}{5}\) \(=30\) 次に平均の2乗を求めます。 Cクラスの平均点は60点なので、 \(60^{2}=3600\) 分散\(s^{2}==280\) したがって、求める分散は280である。 日経平均株価 関連ニュース 外為17時 円、3日ぶり反落 110円台前半 対ユーロも安い (1730) 裁定取引の現物株買い残、3週ぶり増加 16日時点 (1627




Gogogo 待ち行列の計算はコレだけ覚えておくこと




平均 時速 数学クイズ 往復の速さを考える少女 で確実にだまされる Amp Petmd Com
標準偏差を求めるには、 分散 (それぞれの数値と平均値の差の二乗平均)の正の平方根を取ります 。 データが平均値の周りに集中していれば標準偏差は小さくなり、逆に平均値から広がっていれば標準偏差は大きくなります。 標準偏差 s s は、次の公式で求めることができます。 標準偏差 s s を求める公式 s = √s2 = ⎷ 1 n n ∑ n=1(xi −¯¯¯x)2 s = s 2 = 1 n ∑ n = 1 n ( x excel表格平均值公式 sikoyu 第四步:然后,我们输入"=AVERAGE(A13)",这个公式代表我们对到A13单位格的数字进行取均值。平均流速(へいきんりゅうそく)を求める実用的な公式は、「マニングの公式」「シェジーの公式」「クッタの公式」があります。 特に「マニングの公式」は、簡単な計算で精度よく平均流速を計算できることから「流速公式の王様」と呼ばれています。 今回は平均流速の公式、種類、意味について説明します。 平均流速の意味、マニングの公式の詳細は下記が




度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




標本平均と標本分散とは 具体例と性質 証明付 理数アラカルト
平均值有算术平均值,几何平均值,平方平均值(均方根平均值,rms),调和平均值,加权平均值等,其中以算术平均值最为常见。 求平均值的公式 文/ 对几何平均,也可以像算术平均一样,做加权的几何平均。 简单几何平均的计算公式为: 即,n 个数据相乘后开 n 次方。其中,x i 都是正实数。 几何平均适用于对比率、指数等进行平均,主要用于平均增长(变化)率,对数正态分布。 算术几何平均数Amazonで日本経済新聞社インデックス事業室の株がわかる! 日経平均公式ガイドブック 第2版 (日本経済新聞出版)。アマゾンならポイント還元本が多数。一度購入いただいた電子書籍は、KindleおよびFire端末、スマートフォンやタブレットなど、様々な端末でもお楽しみいただけます。




例題 平均値と仮平均 Youtube




相加相乗平均まとめ 公式 証明 使い方 最小値 等号成立 理系ラボ
解答 (1) このデータの平均値は、 \begin {align} \overline {x} &= \frac {18 29 24 42 7 36} {6} \\ &= \frac {156} {6} \\ &= 26 \end {align} 分散の公式より、 s^2 = \displaystyle \frac {1} {6} \ { (18 − 26)^2 (29 − 26)^2 (24 − 26)^2 (42 − 26)^2 (7 − 26)^2 (36 − 26)^2\}また,流積は台形の面積の公式から (1610)×4÷2=52 で a= 52 (m 2 ) となります. ここで,流積 aを潤辺 s で割った値を径深(記号はr,別名水理学的平均水深)といいます.平均値(へいきんち)とは、データの値の合計をデータの総数で割った値です。 身近な例が「試験の点数」ですよね。 「70点、80点、85点、65点、90点」という点数の平均値は、「 ()÷5」で算定します。 平均値を算定すればデータの特徴や傾向が「ある程度」わかります。 一方で問題点もあります。 例えば「50点、50点」の点数の平均値は50点ですが、
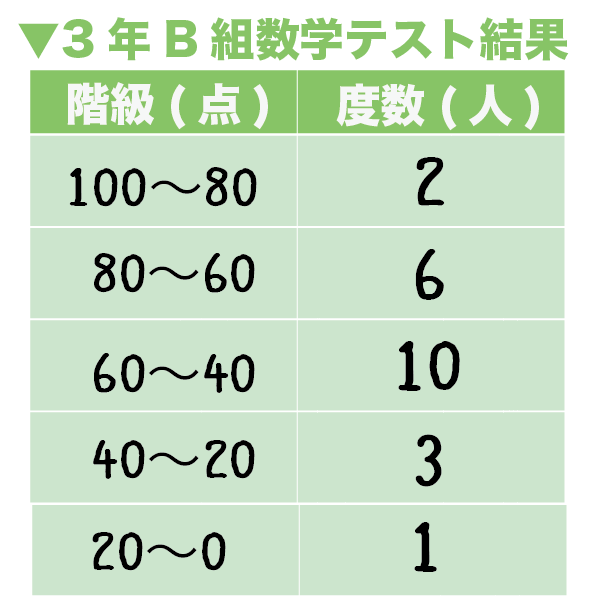



度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




小5算数の宿題 仮の平均 を使って平均を求める方法 がんばるブラザーズ
ときの平均点はいくつでしょうか。 この時、2つの中学校の平均点を平均 すると「(60点+40点)÷2=50点」 になります。しかし、今回のように各中学校の生徒数が異なる場合は、工夫が必要になります。そ こで登場するのが加重平均です。一般に,離散変量における (算術)平均は次のように拡張されます。 確率変数 X が左の表で示される確率分布に従うとき,次の式の右辺で与えられる値を,確率変数 X の 期待値 または 平均値 といい,E (X) または で表す。 E (X) = = x1p1x2p2xkpk このとき,p1p2pk=1 であることに注意して下さい。 また, のとき,ちょうど算術平均となります。 この形を,連続大人の平均身長と平均体重 身長・体重の全国平均 (18年公開の総務省データ)と比較します。 ※計算結果や情報等に関して当サイトは一切責任を負いません。 また個別相談は対応しません。
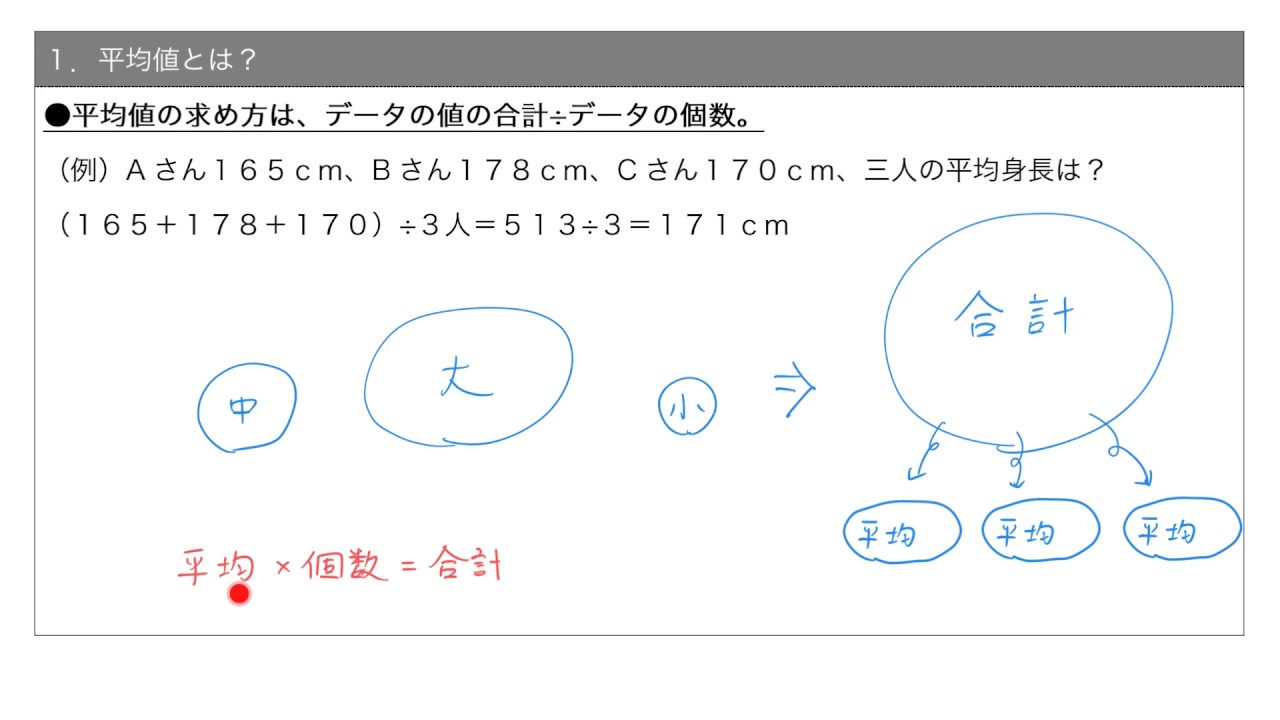



要点 平均値と仮平均 Youtube




平均 分散 標準偏差とは 後編 株式会社neoclassic
5 二項分布の平均と分散 二項分布B(n, p) の平均と分散は 平均:µ = E(X)=np 分散:σ2 = V(X)=npq = np(1−p) 6 確率変数の和の平均 確率変数の平均について次の公式が成り立つ。 E(X Y)=E(X)E(Y) 7 互いに独立な確率変数の積の平均 互いに独立な確率変数X, Y に対して平均 値は集団の 2乗が都合がよいでしょう。また、これとは別に2乗する事によって統計上のいろいろな公式と関連させられるので都合が良いのです。(解説) 平均値 e(x) という1種類の代表値だけでは,元のデータの散らばり具合が表せません. 次の図1の上の図と下の図とでは,平均値が同じですが,上の図ではデータが平均値付近に集まっているのに対して,下の図ではデータは散らばっており,これら2つのデータは異なる傾向を持ってい



データの分析を総まとめ 公式の覚え方や裏ワザ 重要記事一覧 受験辞典




高校数学 分散s と標準偏差s 分散の別公式 受験の月




高校数学 平均値 と 平均値のとりうる値 例題編 映像授業のtry It トライイット
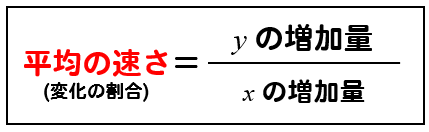



中3 数学 平均の速さの求め方を解説 数スタ




3 T1 T2間の平均の加速度を求めよ Clear




平均値とは 求め方が一瞬でわかる 中央値との違いも解説 高校生向け受験応援メディア 受験のミカタ



相加相乗平均の証明から使い方までを丁寧に解説 数学の面白いこと 役に立つことをまとめたサイト




往復の平均の速さ 間違えずに求められますか




相乗平均 幾何平均 の意味 図形的イメージ 活躍する例 具体例で学ぶ数学




算数上第4回 和差算 もりのひと小学校




Cagr 年平均成長率 とは 意味やエクセル計算式を徹底解説 すべての投資家達へ 暗算 習う 解説
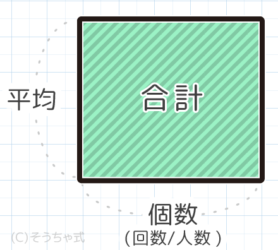



中学受験 平均算の解き方 面積図の書き方は 分かりやすく図解 そうちゃ式 受験算数 新1号館




平均の加速度と等加速度直線運動の見分け方を教えてください どっちの公式を使えばいいの Clear
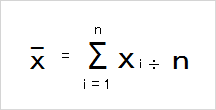



S シグマ を使った平均値の計算式 統計学が わかった
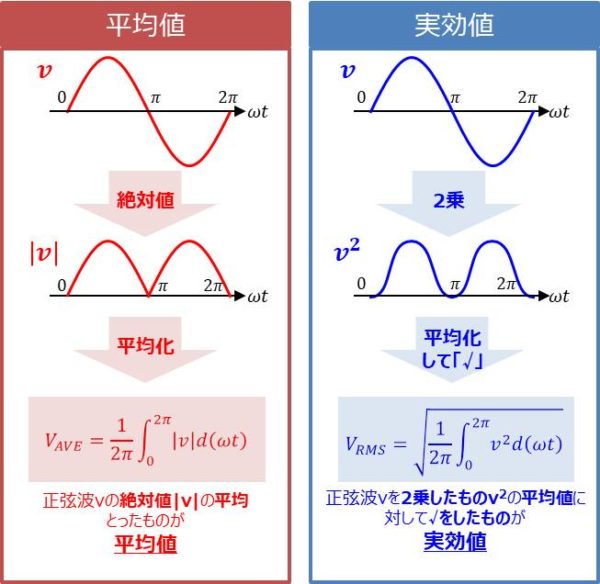



平均値 と 実効値 の違いについて 詳しく説明します




小学校5年 算数 平均の表し方 Youtube
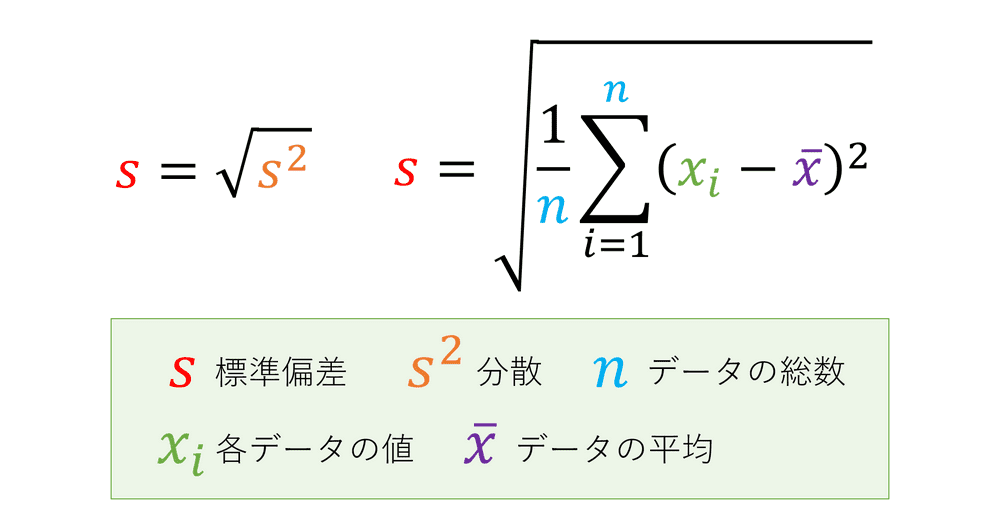



標準偏差をエクセルの関数で求める方法とグラフの作り方 散布図 Office Hack




標準化 変量の変換 とは 仮平均についてもわかりやすく解説します 遊ぶ数学




相加相乗平均まとめ 公式 証明 使い方 最小値 等号成立 理系ラボ



加重平均 加重移動平均 指数移動平均とは 制御工学の基礎あれこれ




小5 算数 小5 21 平均 Youtube




平均変化率と微分 微分係数との関係をわかりやすく解説 ネットdeカガク



分散とは 公式 求め方や計算問題 分散分析 多重比較の意味も 受験辞典




算術平均 相加平均 と加重平均の違いは 重み ってナニ データ分析の解説 Haku1569 Excel でらくらく データ分析
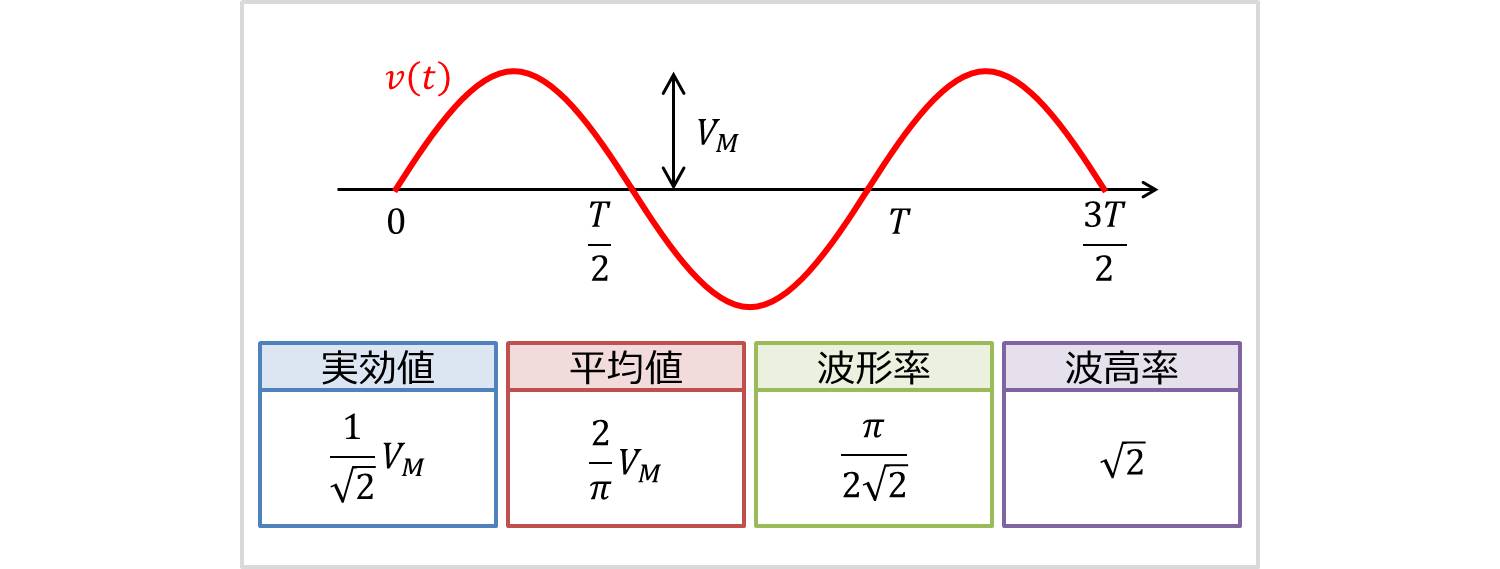



正弦波 の実効値 平均値 波形率 波高率の求め方 Electrical Information




平均値 中央値 最頻値の求め方といくつかの例 高校数学の美しい物語




統計学 第3回 西山 第2回のまとめ 確率分布 決まっている分布の 形 期待値とは平均計算 平均 合計 個数から卒業 平均 割合 値の合計 同じ平均値でも 同じ分散や標準偏差でも Ppt Download




中1数学 平均点の求め方 Youtube



3




数学 行き 時速80 帰り 時速 往復の平均時速は 温故知新ラーニング 楽天ブログ



1




一応理科の宿題です 二問とも答えは書いたんですけど Clear




標準偏差とは何か その求め方や公式の意味 使い方をわかりやすく説明します アタリマエ




相加相乗平均とは 公式 証明から使い方までが簡単に理解できます 練習問題付き 高校生向け受験応援メディア 受験のミカタ



小5算数の宿題 仮の平均 を使って平均を求める方法 がんばるブラザーズ




Tvアニメ 私 能力は平均値でって言ったよね 公式サイト



3
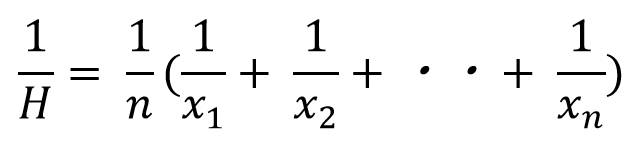



中学数学 理科 調和平均の考え方 速さから合成抵抗まで 偏差値40プログラマー
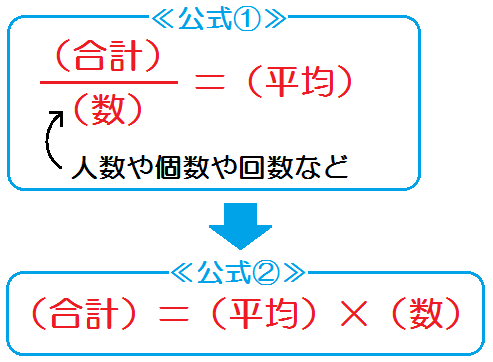



中学数学 1次方程式 文章題の解き方 平均




統計学 第4回 西 山 Ppt Download



Studydoctor平均値と仮平均での求め方 高校数学 Studydoctor
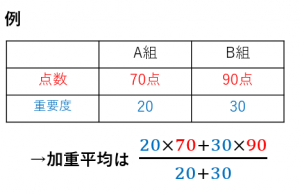



加重平均 重みつき平均 の例と意味 具体例で学ぶ数学
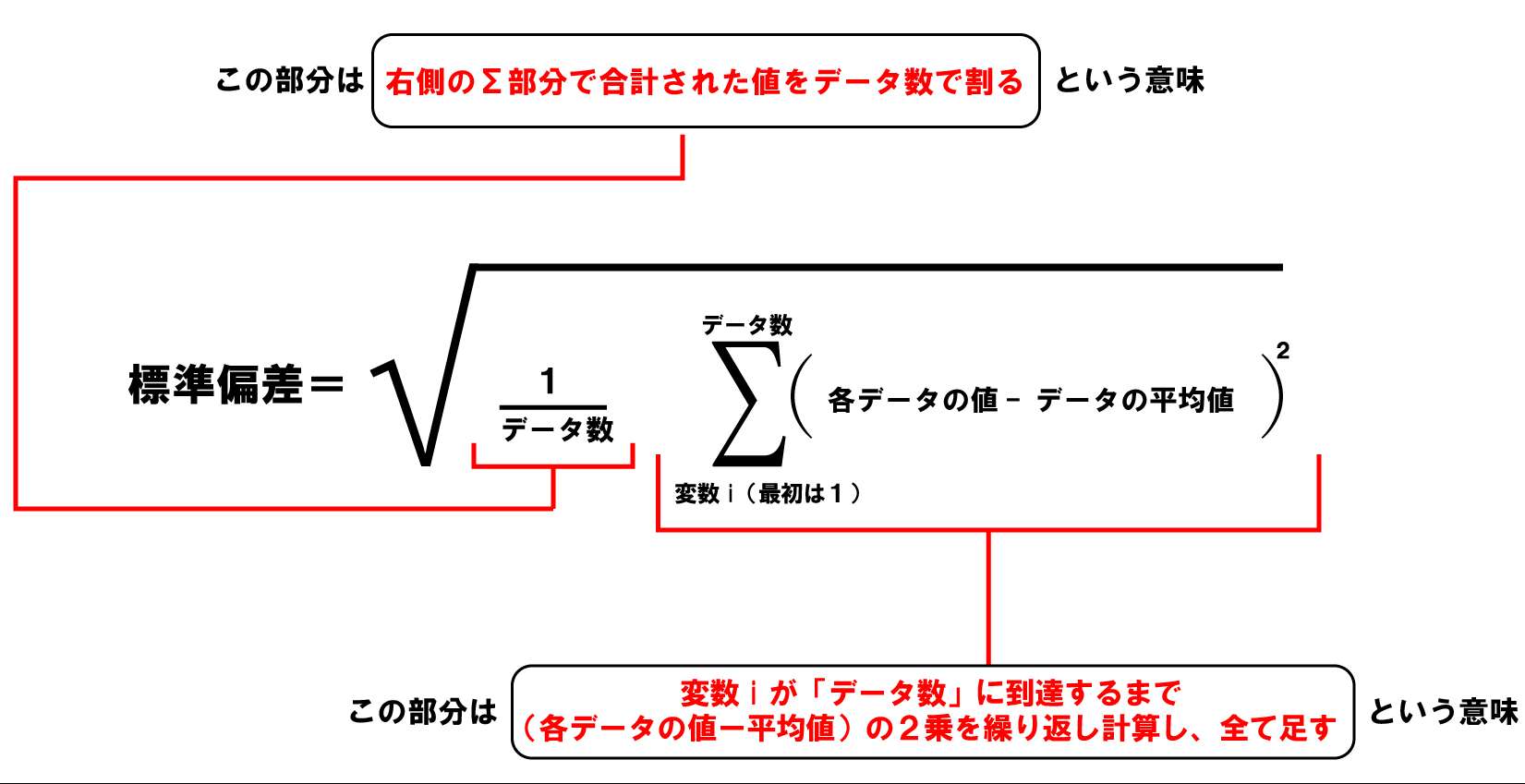



標準偏差とは 意味から求め方 分散との違いまでわかりやすく解説




統計学 第3回 西山 第2回のまとめ 確率分布 決まっている分布の 形 期待値とは平均計算 平均 合計 個数から卒業 平均 割合 値の合計 同じ平均値でも 同じ分散や標準偏差でも Ppt Download




平均の速度と瞬間の速度の違いとは 公式および求め方



ゆーノッポのモノ作りのアレコレ Ssブログ




センター試験頻出 分散とは 求め方や意味を徹底解説 高校生向け受験応援メディア 受験のミカタ



32 3 移動平均 統計学の時間 統計web
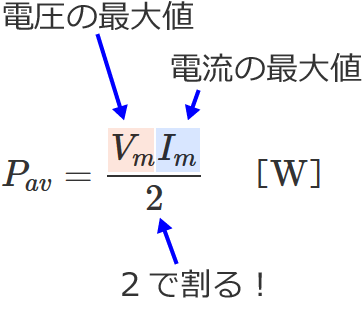



交流回路の電力の計算 抵抗だけの回路
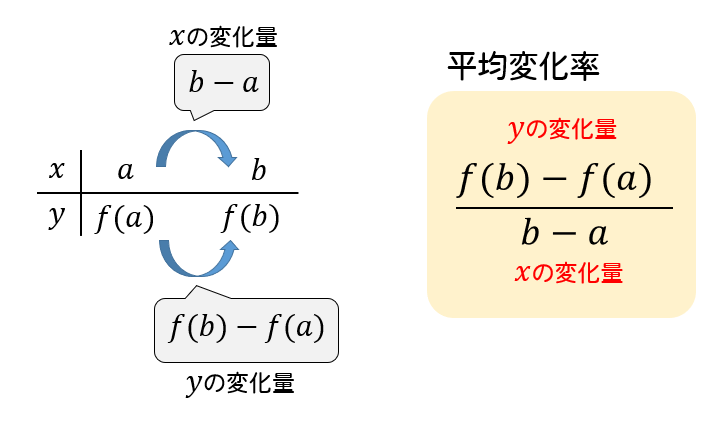



平均変化率とは 公式がややこしく見えるけど大丈夫 わかりやすく解いてみよう 数スタ




算術平均 幾何平均 加重平均の計算 With Excel
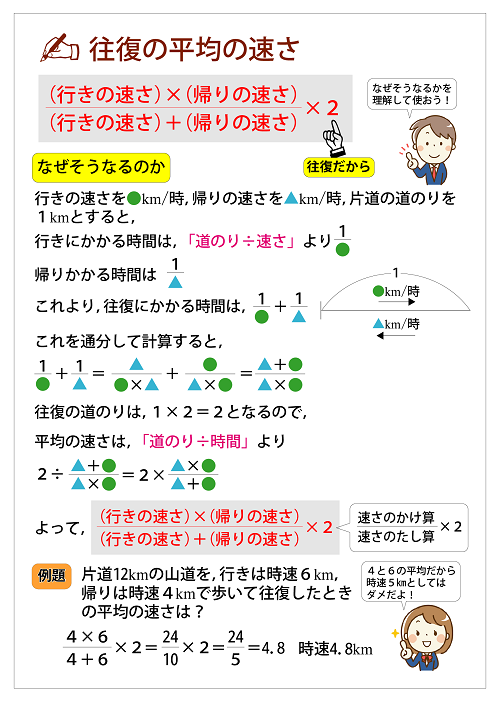



往復の平均の速さに関する公式のカードを作りました 恋する中高一貫校 適性検査 徹底攻略




高校数学 分散 とは 練習編 映像授業のtry It トライイット




平均 算数用語集



1
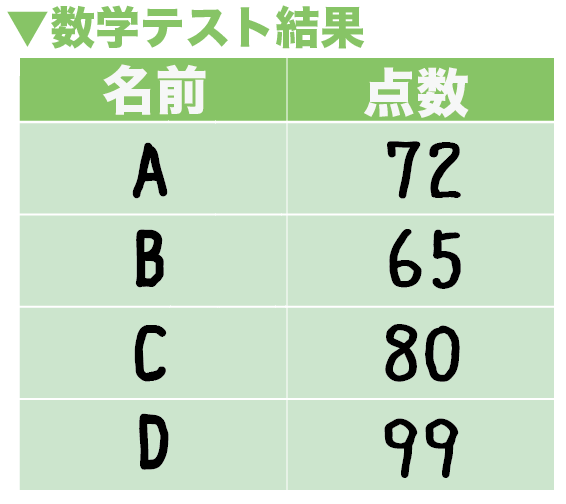



度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




小学生算数 平均算のやり方を1からていねいにやってみよう 数スタ
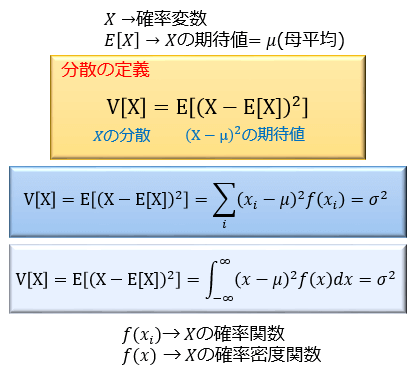



分散の求め方と公式 その有用性について アタリマエ




小学5年生の算数 平均の求め方 練習問題プリント ちびむすドリル 小学生




相加平均 相乗平均 基本編 おいしい数学
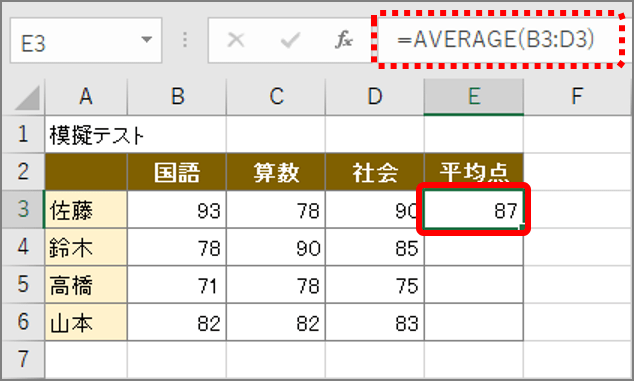



エクセル 平均 を簡単に求めよう いまさら聞けない平均算出ワザ3選 Getnavi Web ゲットナビ
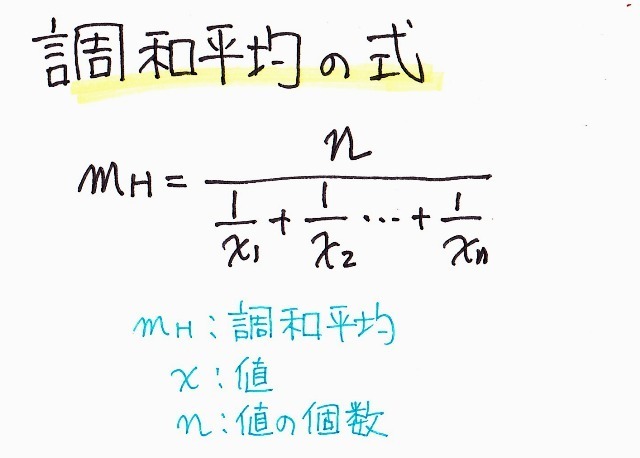



調和平均とは データ分析の解説 Haku1569 Excel でらくらく データ分析



平均流速公式 等流 不等流 マニングの式 P408




平均の求め方 小学生で学ぶ公式は 問題の解き方を解説 中学数学 理科の学習まとめサイト




平均値と中央値の違いとは 意味や特徴や数式などを簡単にわかりやすく いちばんやさしい 医療統計




標本平均と標本分散とは 具体例と性質 証明付 理数アラカルト



流速とは 1分でわかる意味 単位 平均流速との関係 マニングの公式



2




度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




中学数学 平均値と中央値の3つの違い Qikeru 学びを楽しくわかりやすく




平均の求め方
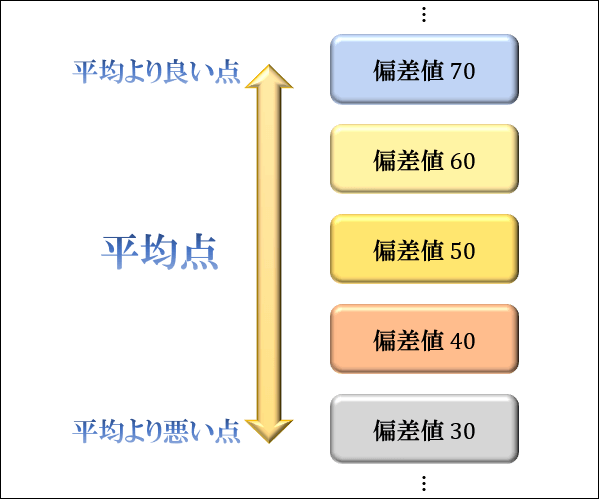



偏差値とは何か 図解でわかるその意味と使い道 求め方 アタリマエ




しっかり区別しよう 平均の速度と瞬間の速さ 物理のいろは




資料のちらばりと代表値 度数分布表からの平均値の求め方 中学数学 定期テスト対策サイト




相関係数とは何か その求め方 公式 使い方と3つの注意点 アタリマエ




中学数学 3分でわかる 平均値の出し方 Qikeru 学びを楽しくわかりやすく




ヒストグラムを使った平均値の求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




二乗平均速度と根二乗平均速度の公式と計算方法




平均から数を求める Youtube
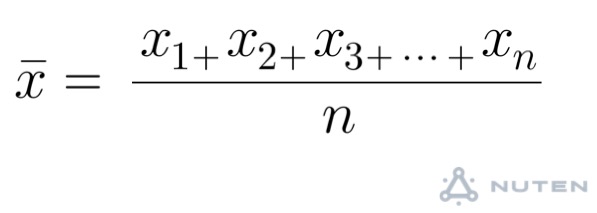



数学的ジョーク テストの平均点を少し高く見せる方法 Steemit




中1文字式 平均の表し方を解説 Youtube




平均分子量とは 求め方や入試問題でどう使うかをまとめてみた 化学受験テクニック塾




中学数学 3分でわかる 平均値の出し方 Qikeru 学びを楽しくわかりやすく



平均値と期待値の違い 制御工学の基礎あれこれ




標本平均と標本分散とは 具体例と性質 証明付 理数アラカルト
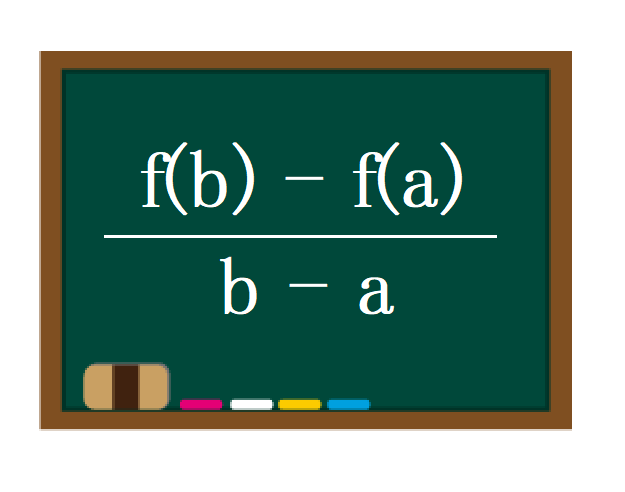



平均変化率の求め方 どんな関数でも公式一つで簡単に ヒデオの情報管理部屋
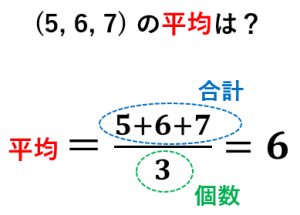



平均の求め方 計算式 と意味 欠点 具体例で学ぶ数学




算数の公式 教育 プリントアウトファクトリー Myricoh
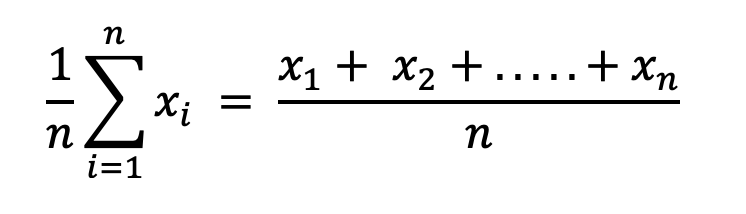



算術平均 幾何平均 中央値 最頻値の意味 違い 使い方




分散公式 2乗の平均 ー 平均の2乗 Youtube



平均の速さの求め方は 1分でわかる計算 公式 意味 はじきとの関係



流速とは 1分でわかる意味 単位 平均流速との関係 マニングの公式
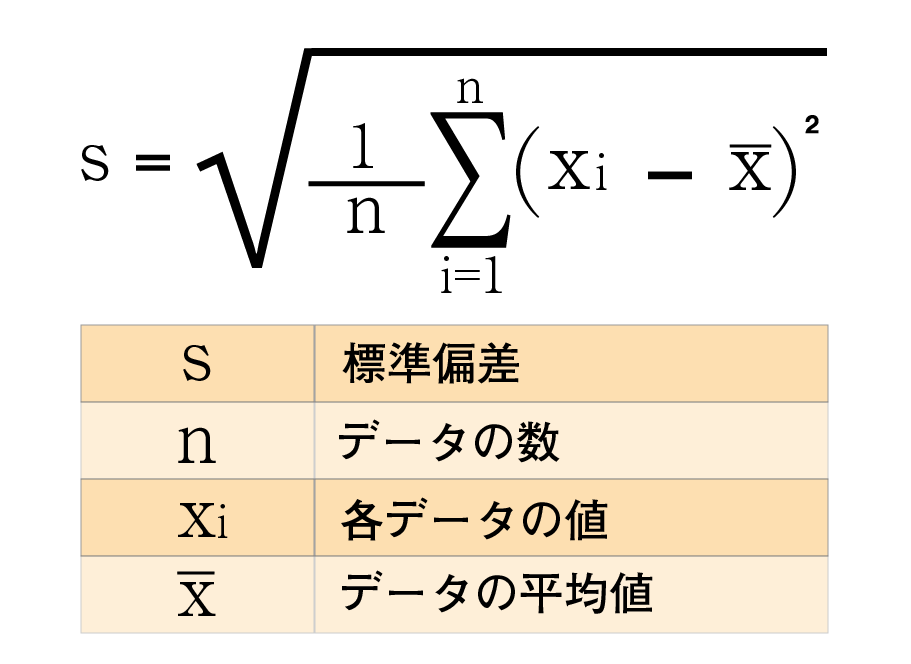



標準偏差とは 意味から求め方 分散との違いまでわかりやすく解説



データの分析を総まとめ 公式の覚え方や裏ワザ 重要記事一覧 受験辞典


